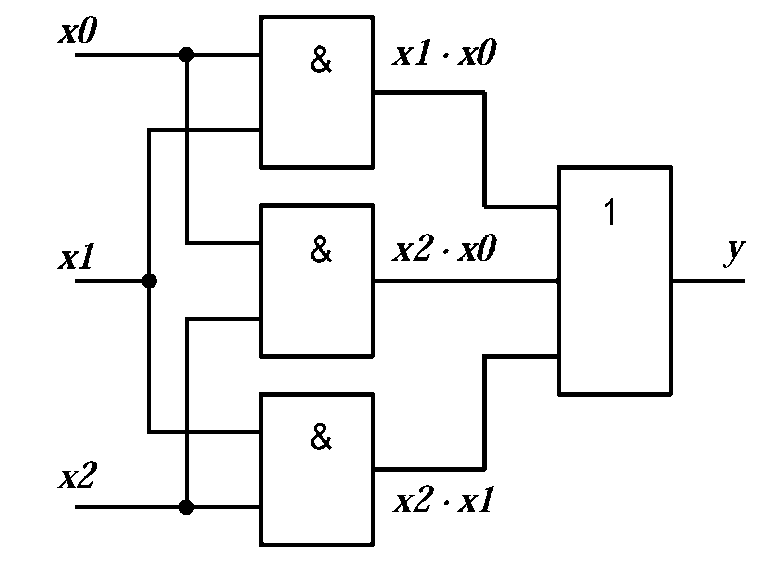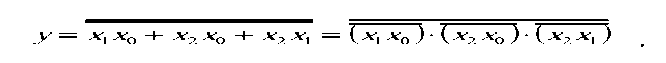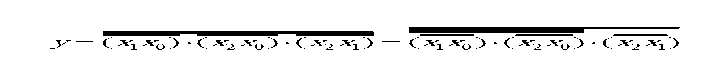2.7. Реализация функции в заданном логическом базисе
Наиболее простой является реализация функции в базисе (И, ИЛИ, НЕ). Реализация оптимальным набором элементов означает, что можно использовать элементы с любым необходимым количеством входов (до восьми); схема устройства для функции из рассматриваемого примера показана на рис. 2.6.
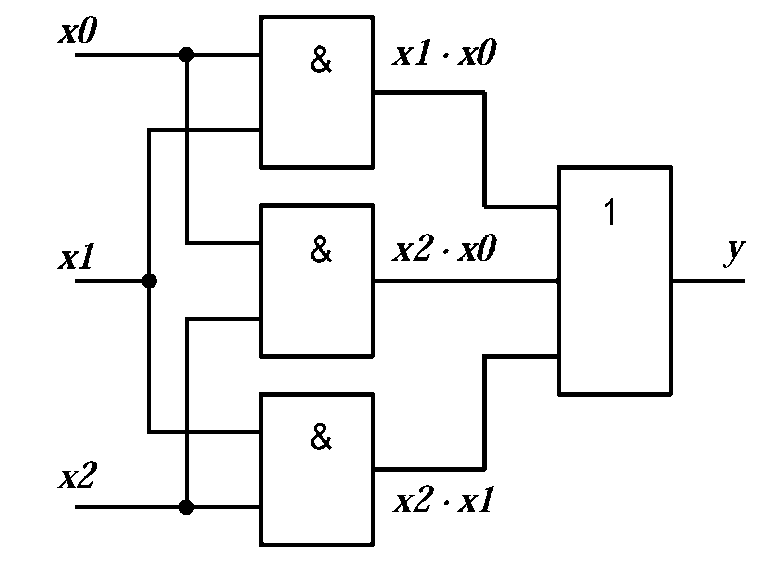
Рисунок 2.6 - Реализация функции из примера в базисе (И, ИЛИ, НЕ).
Для построения схемы в базисе (И-НЕ) необходимо преобразовать логическое уравнение, используя двойное отрицание и правило де Моргана
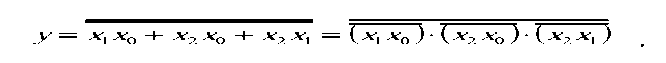
Как видно, полученное выражение содержит только операции конъюнкции и инверсии, что согласуется с заданным логическим базисом. Схема устройства в соответствии с этим выражением представлена на рис. 2.7.
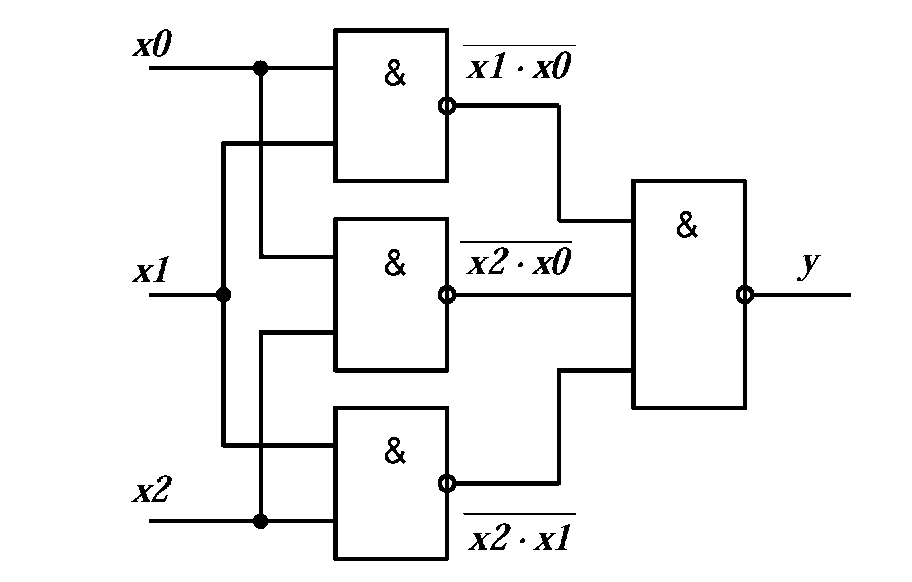
Рисунок 2.7 - Реализация функции из примера в базисе (И-НЕ).
Если требуется реализовать функцию из однотипных элементов в определенном базисе (например, (И-НЕ)), то трехвходовый элемент на рис.2.7 нужно заменить группой двухвходовых в соответствии с выражением:
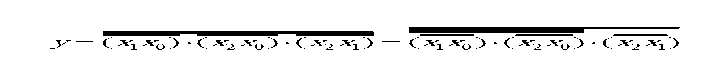
Реализация этого выражения представлена на рис.2.8.
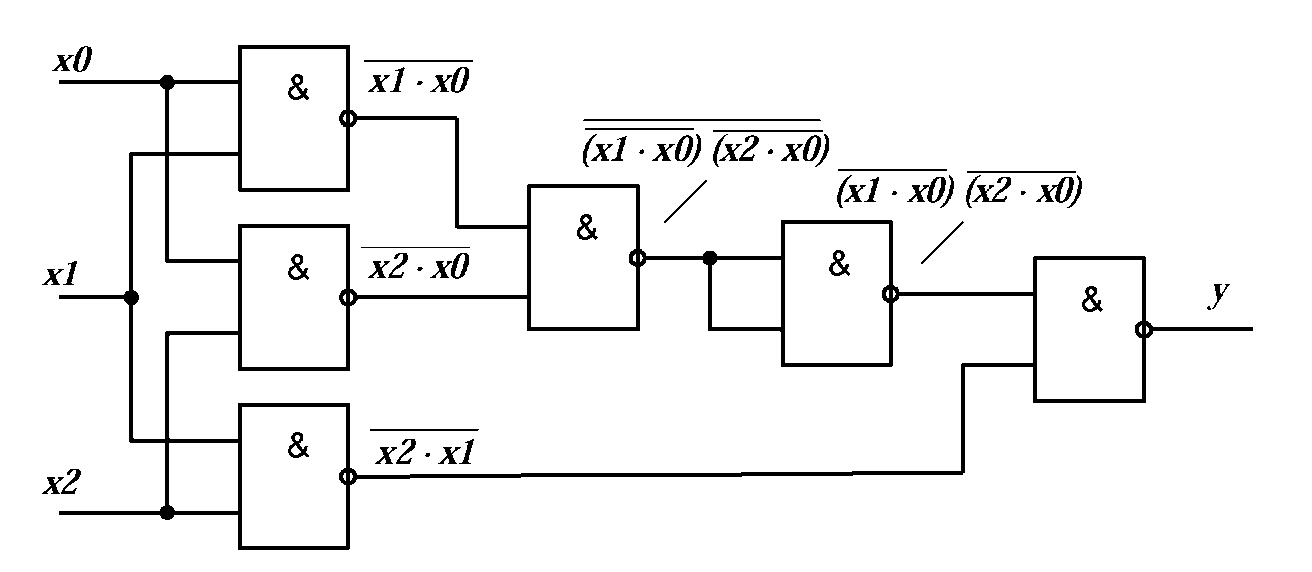
Рисунок 2.8 - Реализация функции из примера в базисе (И-НЕ) только на двухвходовых элементах 2И-НЕ.
Правильный выбор логического базиса для реализации логической функции, как правило, позволяет сократить количество микросхем при изготовлении физического цифрового устройства.
|