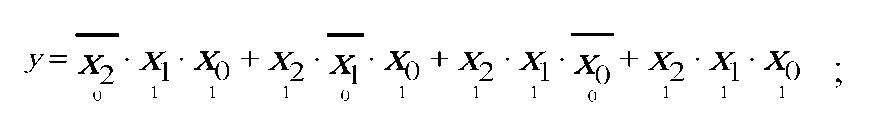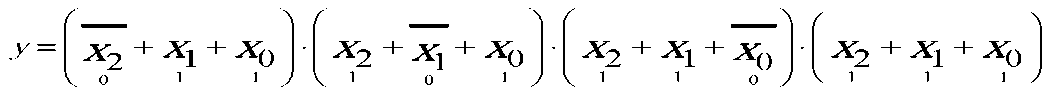2.3. Способы задания логических функций. Словесный, табличный и аналитический способы
1) Словесный. В словесной форме выражается взаимосвязь между аргументами функции и ее значениями.
Пример: функция трех аргументов принимает значение "1", когда любые два или более аргументов функции равны "1".
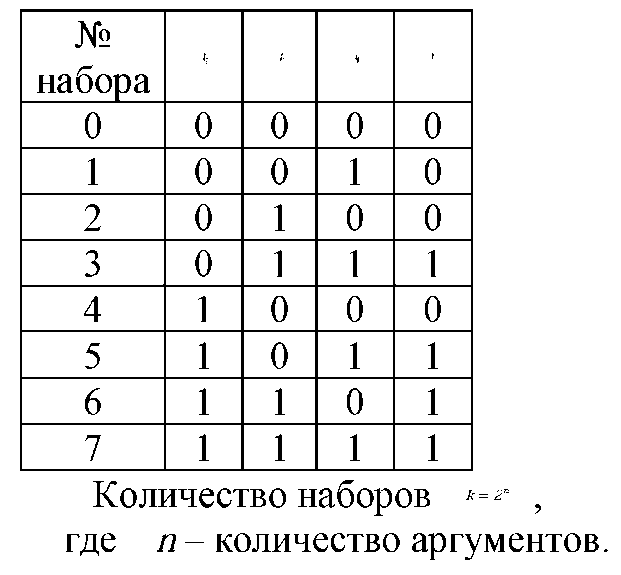
2) Табличный. Состоит в построении таблицы истинности, содержащей
значения функции для всех наборов значений аргументов.
3) Аналитический. Функция задается в виде алгебраического уравнения, в котором логические переменные связаны логическими операциями. Используются две формы записи:
ДНФ - дизъюнктивная нормальная форма - это логическая сумма элементарных логических произведений аргументов. Каждое логическое произведение образуется таким набором аргументов, для которого функция равна 1. В данном примере по таблице истинности получаем такую запись в виде ДНФ:
 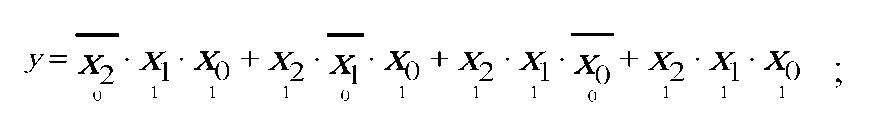
КНФ - конъюнктивная нормальная форма - это логическое произведение логических сумм аргументов; для функции из примера получаем:
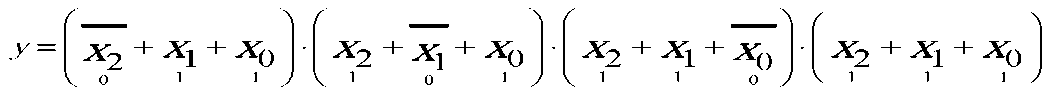
Если в каждом произведении в функции вида ДНФ присутствуют все аргументы функции, то такая запись называется СДНФ - совершенная ДНФ. Входящие в запись произведения называются минтермами.
Если в суммах функции вида КНФ участвуют все аргументы функций, то такая запись называется СКНФ - совершенная КНФ, а сами суммы - макстермами.
Функция может быть записана в КНФ в виде суммы произведений, но при этом каждое произведение характеризует нулевые значения функции.
|