Микропроцессоры и микроконтроллеры

Особенности реализации табличных функций

В дисциплинах, связанных с изучением численных методов (информатика, исследование операций) рассматривается классический метод линейной интерполяции. Согласно нему, значение функции в произвольной точке Х находится на основании значений функции в двух ближайших узлах интерполяции: Хi≤ X ≤ Xi+1. Функция задается в виде массива значений аргумента и соответствующих значений функции. Перед вычислением значения функции необходимо найти соответствующий отрезок между узами интерполяции. Применение этого метода требует поисковой процедуры и интерполяционных вычислений.

В некоторых случаях можно существенно упростить интерполяционную процедуру. Предпосылками этого являются:

·        невысокие требования по точности, когда значение функции между узлами интерполяции можно заменить значением в узле;

·        критичности по времени нахождения результата;

·        набор значений аргументов можно заменить набором порядковых индексов; иногда для этого используют не абсолютные, а “взвешенные” относительные значения аргумента;

·        функция представляет собой метод перекодировки значений, когда упорядоченному набору значений аргумента ставится в соответствие фиксированный набор значений функции, а промежуточные (межузловые) значения в принципе невозможны.

Классическим примером является формирование кодов управления семисегментным индикатором. В этом случае по входному аргументу от 0 до 15 нужно формировать байтовый код для индикатора (7-й бит – сегмент “р”, 6-й бит – сегмент “g”,…, 0-й бит – сегмент “a”). Набор значений аргументов формируется в соответствии с таблицей:

Программная реализация функции должна позволять выполнить доступ к массиву значений по индексу, который непосредственно является аргументом функции. Сам массив значений можно хранить в памяти программ как дополнение к телу функции. Массив значений аргумента при этом не нужен.

При реализации такого подхода для MCS-51 удобно воспользоваться командой чтения константы из памяти программ: MOVC A,@A+DPTR. При этом адрес памяти программ, из которого читается константа, будет вычислен как сумма содержимого А и текущего значения регистра DPTR. Т.е. значение DPTR является базовым адресом начала массива. Сам массив значений может располагаться в любом месте памяти программ (до или после подпрограммы определения функции).

mov a,#3 ; задание нужного индекса (начиная с 0)

call F1 ; вызов подпрограммы

jmp $ ; “цикл” – прочие команды

; таблица значений функции (константы в памяти программ)

table: db3Fh,06h,5Bh,4Fh,66h,6Dh,0FDh,07h,7Fh,6Fh,77h,7Ch,39h,5Eh,79h,71h

; подпрограмма получения значения функции по аргументу-индексу

F1: mov dptr,#table ; задание адреса таблицы

movc a,@a+dptr ; чтение элемента таблицы в аккумулятор

ret ; возврат из подпрограммы

В результате выполнения приведенного фрагмента подпрограмма F1 вернет в аккумуляторе значение 4Fh (элемент с индексом 3 при нумерации, начиная с 0).

Единственный недостаток данной подпрограммы – необходимость использования регистра DPTR, который может быть занят для других целей.

Альтернативным вариантом решения является использование относительной адресации таблицы. Этот подход основан на том, что таблица значений функции может располагаться в памяти программ непосредственно после команды RET, т.е. положение таблицы может быть точно определено относительно определенных операторов внутри подпрограммы (при этом абсолютный адрес таблицы знать не нужно). Чтение элемента таблицы выполняется командой MOVC A,@A+PC. При этом адрес памяти программ, из которого читается константа, будет вычислен как сумма содержимого А и текущего значения регистра PC.

mov a,#3 ; задание нужного индекса (начиная с 0)

call F1 ; вызов подпрограммы

jmp $ ; “цикл” – прочие команды

; подпрограмма получения значения функции по аргументу-индексу

F1: inc a ; коррекция индекса (учет команды RET)

movc a,@a+pc ; чтение элемента таблицы в аккумулятор

ret ; возврат из подпрограммы

; таблица значений функции (константы в памяти программ)

table: db3Fh,06h,5Bh,4Fh,66h,6Dh,7Dh,07h,7Fh,6Fh,77h,7Ch,39h,5Eh,79h,71h

При чтении команды MOVC A,@A+PC из памяти перед ее выполнением в регистре PC формируется адрес следующей команды, т.е. однобайтовой команды RET. Адрес начала таблицы на 1 больше адреса команды RET. Именно это учитывается с помощью команды INC A, которая корректирует заданный индекс (смещение от начала таблицы до нужного элемента). Эта подпрограмма не использует никакие дополнительные регистры. Заметим, что значение адреса таблицы явно не используется.

Еще один пример использования указанного подхода – реализация функции sin(x). Пусть аргумент функции изменяется в пределах от 0 до p, и, следовательно, значение функции изменяется от 0 до 1 и опять до 0. Значение аргумента и результат можно представлять в однобайтовом формате. В таком случае аргумент может принимать 256 различных значений, и вес единицы младшего разряда в представлении аргумента составляет (p/255). При представлении значений функции будем полагать, что запятая располагается перед старшим разрядом, т.е. значению 0 соответствует двоичный код 00000000, а значению 1 – код 11111111. Набор значений функции может быть получен итерационным расчетом по следующей формуле:

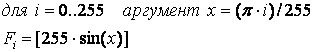
где [ ] – операция получения целой части числа.

Функция получения значения синуса может выглядеть так:

SIN: inc a ; коррекция индекса (учет команды RET)

movc a,@a+pc ; чтение элемента таблицы в аккумулятор

ret ; возврат из подпрограммы

; таблица значений функции – 256 байт

table: db 00h,01h,...,0FEh,0FFh,0FEh,...,01h,00h