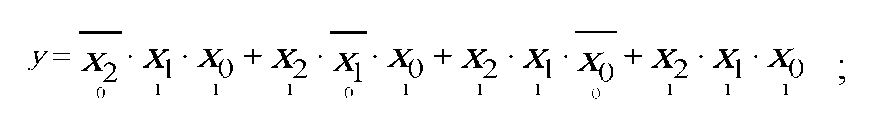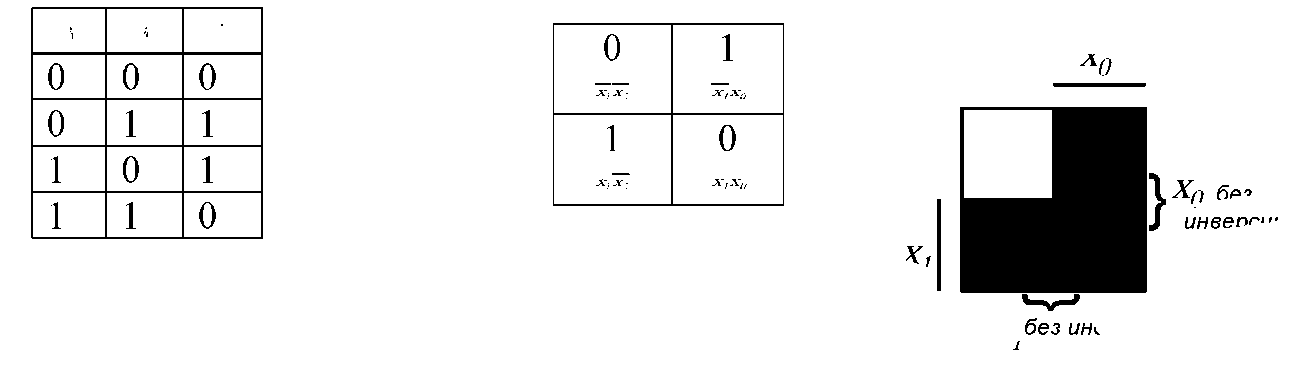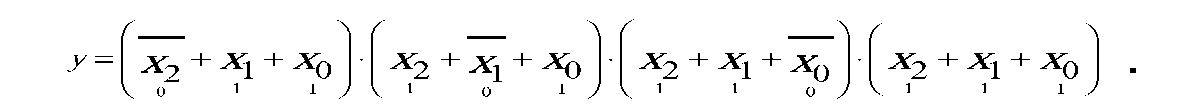2. Описание и минимизация логических функций 2.1. Способы задания логических функций
Описание и минимизация логических функций
Способы задания логических функций
1) Словесный. В словесной форме выражается взаимосвязь между аргументами функции и ее значениями.
Пример: функция трех аргументов принимает значение "1", когда любые два или более аргументов функции равны "1".
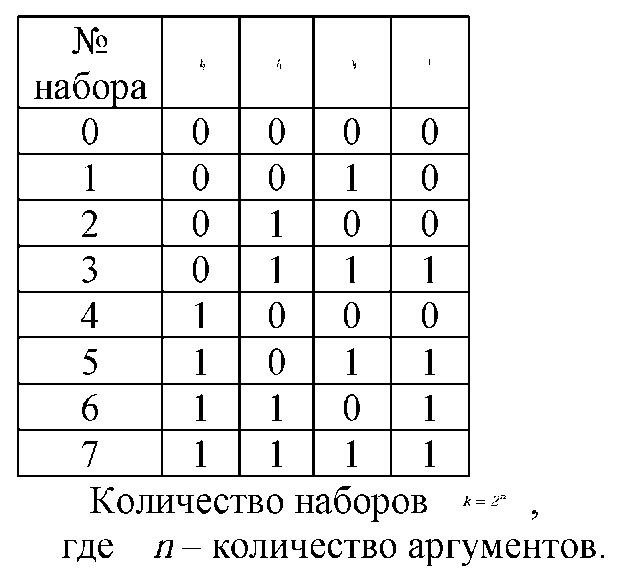
2) Табличный. Состоит в построении таблицы истинности, содержащей
значения функции для всех наборов значений аргументов.
3) Аналитический. Функция задается в виде алгебраического уравнения, в котором логические переменные связаны логическими операциями. Используются две формы записи:
ДНФ - дизъюнктивная нормальная форма - это логическая сумма элементарных логических произведений аргументов. Каждое логическое произведение образуется таким набором аргументов, для которого функция равна 1. В данном примере по таблице истинности получаем такую запись в виде ДНФ:
 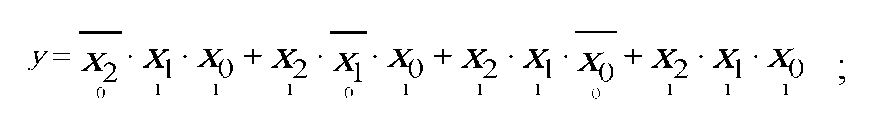
КНФ - конъюнктивная нормальная форма - это логическое произведение логических сумм аргументов; для функции из примера получаем:
Если в каждом произведении в функции вида ДНФ присутствуют все аргументы функции, то такая запись называется СДНФ - совершенная ДНФ. Входящие в запись произведения называются минтермами.
Если в суммах функции вида КНФ участвуют все аргументы функций, то такая запись называется СКНФ - совершенная КНФ, а сами суммы - макстермами.
Функция может быть записана в КНФ в виде суммы произведений, но при этом каждое произведение характеризует нулевые значения функции.
4) Использование карт Карно
Карта Карно - это прямоугольная таблица, содержащая 2 клеток, где • -количество аргументов функции. В каждой клетке проставляют значение функции, соответствующее определенному минтерму. Правило расположения аргументов по таблице такое, что конъюнкции, соответствующие соседним клеткам, отличаются только одним аргументом. Пример заполнения карты Карно для функции двух аргументов, показан на рис. 2.1.
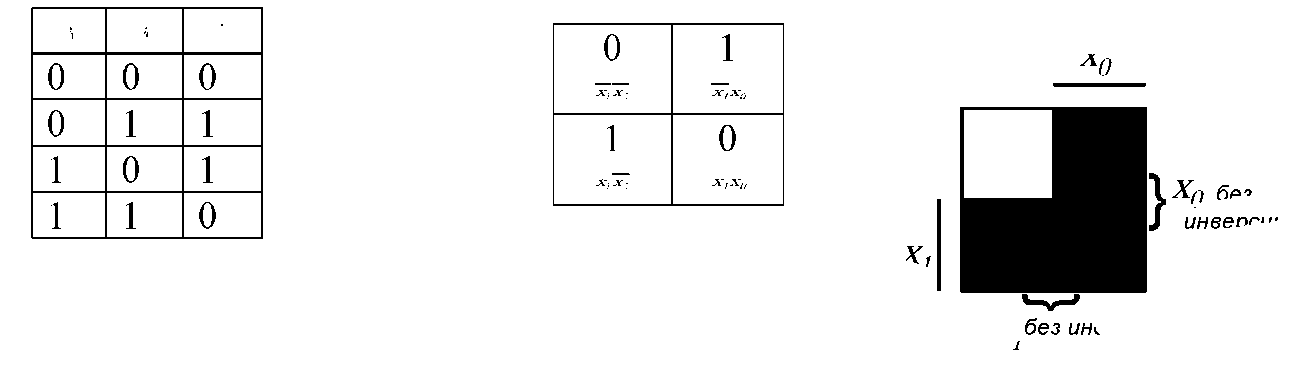
Рисунок 2.1 - Пример заполнения карты Карно для функции двух аргументов
Для каждого аргумента функции можно выделить область на карте Карно, в которой все клетки соответствуют произведениям с прямыми (т.е. неинверсными) значениями этого аргумента. Такие области принято отмечать чертой с указанием рассматриваемого аргумента.
Рис. 2.2. содержит пример заполнения карты Карно для функции трех аргументов. Цифры в правом углу клетки отмечают номер набора значений аргументов, соответствующего данной клетке. Как видно, в каждой клетке проставляется значение функции, соответствующее этому набору.
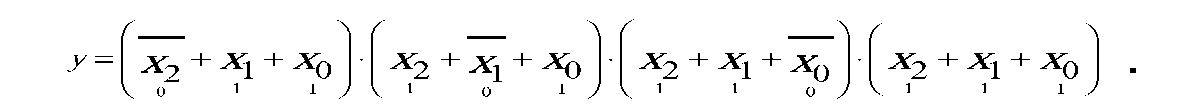
Рисунок 2.2 - Пример заполнения карты Карно для функции трех аргументов
|